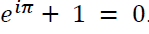
Dla zwykłego śmiertelnika to równanie nie znaczy zupełnie nic, a w każdym razie niezbyt wiele. Może on wprawdzie, zauważywszy ten osobliwy napis przystanąć i zastanowić się nad nim przez chwilę, rozpoznając znajomo wyglądające symbole, działania czy funkcje. Jednak wątpliwe, że wzór ów zdoła na dłużej przykuć jego uwagę. Gdy jednak opodal przechodzić będzie ktoś nieco bardziej zaznajomiony w tajnikach analizy zespolonej, powiedzmy jakiś wielki uczony z okolic XVIII wieku, otóż gdy ten naukowiec zauważy równanie, to z pewnością zatrzyma się, zaciekawiony podejdzie bliżej i zamyśli się lub nawet cicho westchnie z zachwytu, bo oto ujrzał piękno w najczystszej postaci.
Meloman na koncercie muzyki klasycznej odczuwa radość słuchając mozartowskich symfonii. Słyszy piękno: zestrojenie melodyjnych linii, harmonię, przyjemnie brzmiące, ciepłe barwy orkiestrowe. Można powiedzieć, że jest to piękno zmysłowe: nie musi on myśleć, rozumować słuchając muzyki (choć oczywiście może), ale żeby czerpać z niej przyjemność, wystarczy, że chłonie ją zmysłami. Przyznajmy uczciwie, że muzyka XX i XXI wieku nie oferuje mu zbyt wielu podobnych doznań, co nie znaczy oczywiście, że nie jest piękna. Jest, ale w inny sposób – Andrzej Chłopecki mawiał, że Varèse czy Xenakis są klasykami dźwięków „pięknych inaczej”. Problem pojawił się już u Schoenberga, albo nawet chwilę wcześniej, gdy na twarzy naszego melomana wyraz błogiego uśmiechu zastąpił przykry grymas. Z początku sądzono, że to efekt przesadnej intelektualizacji lub – o zgrozo! – matematyzacji procesu komponowania muzyki. Później było jeszcze gorzej: prekompozycyjne spekulacje, permutacje serii, rachunek prawdopodobieństwa czy komputerowe algorytmy. A gdzie harmonia? gdzie przyjemnosć? Bo jeżeli w tej muzyce istnieje jakieś piękno, to chyba wyłącznie natury intelektualnej, a zmysłowa – już tylko brzydota.
Przywołany na początku wzór, znany jako tożsamość Eulera, uważany jest za najpiękniejsze równanie świata. Z pozoru nic w nim szczególnego: ot szereg matematycznych symboli, które lubią umykać z pamięci w najmniej sprzyjającym momencie. Zauważmy jednak, że w tym wyjątkowo krótkim i prostym wzorze pojawiają się wszystkie najważniejsze w matematyce liczby: 0, 1, liczba , e – tzw. liczba Eulera, będąca podstawą logarytmu naturalnego (wynosząca około 2,72) oraz i – jednostka urojona (jej kwadrat jest równy -1). Zostają one połączone trzema podstawowymi działaniami arytmetycznymi: mnożenia, dodawania i potęgowania. Niezwykłe. I wręcz nieprawdopodobne. To jakby będąc w wielkiej bibliotece wybrać dla zabawy po jednym zdaniu z każdej księgi i nagle odkryć, że słowa te nie tylko do siebie pasują, ale również układają się razem we wspaniałą i mądrą opowieść. Opowieść, której abstrakcyjne piękno objąć można jedynie intelektem.
Kakofonia, szumy, zgrzyty. Nie każdy dźwięk może być piękny, a przynajmniej nie od razu. Truizmem jest stwierdzenie, że muzyka w kontekscie nowego czasu nabiera znaczenia nowego: czym innym był Webern dla sobie współczesnych, czym innym dla serialistów, zaś obecnie jego muzyka znaczy dla nas jeszcze coś innego. To, co ignorowane, z czasem może okazać się wartościowe, to, co szokujące – zaciekawia, a to, co brzydkie, drażniace czy nieprzyjemne zaczyna zachwycać. Brzydota nie wyklucza zatem piękna, nie stanowi jego antytezy. Te dwie kategorie umieszczamy zazwyczaj na przeciwległych biegunach – i być może słusznie, ale – do czasu. Do czasu, gdy brzydota i piękno zaczną się do siebie zbliżać, a może nawet zamienią miejscami – takie przypadki znamy dobrze z historii muzyki XX wieku. Rzeczywistym przeciwieństwem piękna nie jest wiec brzydota, lecz banał: muzyka trywialna, sztampowa nie może dać przyjemności ani zmysłom, ani intelektowi. Nawet nasz meloman słuchając banalnych melodii, czego mu oczywiście nie życzymy, będzie bardziej niż o dźwiękach myślał o tym, jak dyskretnie ukryć ziewanie.
Przyglądamy się bezradnie dwóm końcom długiego sznurka, próbując je niezdarnie połączyć lub związać, stworzyć spójną całość z pozornie obcych sobie elementów. Czasem mijają stulecia, zanim zorientujemy się, że jest to właściwie jeden i ten sam sznurek, którego każda nitka doskonale splata się z innymi – przy okazji zauważając, że zawiązany na supeł sznurek nie będzie całością bardziej, niż jest obecnie. Może zatem wystarczy tylko odkryć miejsce i sposób, w jaki jego włókna łączą się ze sobą? Gorzej, gdy sznurek ma więcej, niż tylko dwa końce… Matematyka opisuje świat tak jak każda inna nauka: dzieli go na kawałki, przygląda się każdemu z osobna i próbuje wyjaśniać, choć świat – trawestując myśl Richarda Feynmanna – o jej poczynaniach nie ma bladego pojęcia. Pitagoras zauważył, że u podstaw harmonijnie brzmiących konsonansów leżą proporcje najprostszych liczb, zawierających się w geometrycznej figurze tetraktysu. On jako pierwszy ukazał przestrzeń, w której te dwa światy stykają się ze sobą, i – trzeba przyznać – jest to miejsce niezwykłej urody. Miejsce, w którym intelektualne piękno matematyki spotyka się i łączy ze zmysłowym pięknem muzyki.
Tekst ukazuje się dzięki wsparciu Urzędu Miasta Poznania











