Matematycy, to specyficzny typ naukowców – cały otaczający ich świat próbują ująć za pomocą liczb, wykresów funkcji lub tablic. Modelują procesy finansowe, podają równania zjawisk fizycznych, a w wolnym czasie szukają strategii wygrywającej w grze w szachy. Dlatego jest oczywiste, że tak ważny aspekt życia, jak muzyka, nie mógł pozostać przez matematyków niezauważony. Na czym polega ten niezwykły związek matematyki i muzyki?
Muzyczne twierdzenie Pitagorasa
Muzykę zaczęto badać za pomocą narzędzi matematycznych już w VI w. p.n.e., a zajął się tym nie byle kto, bo sam Pitagoras (znany każdemu uczniowi z twierdzenia o własnościach trójkąta prostokątnego, którego tak naprawdę nie jest autorem). Założył on w Krotonie szkołę religijno-filozoficzną, która zrzeszała myślicieli i ówczesnych naukowców. Niektórzy mogliby dziś uznać ich za „matematycznych fanatyków”, ponieważ pitagorejczycy twierdzili, że „wszystko jest liczbą”, a każdy element wszechświata można wyrazić za pomocą ułamków. To stąd wywodzi się pojęcie harmonii sfer, koncepcji, będącej połączeniem muzyki i matematyki.
Badania Pitagorasa wykraczały jednak znacznie poza górnolotną, mało realistyczną dla nas filozofię. Stało się tak za sprawą monochordu – instrumentu, który posiadał zaledwie jedną strunę. Dla genialnego matematyka miał jednak ogromną moc. Pitagoras analizował za jego pomocą, jak zmieniają się odległości między dźwiękami (czyli interwały) dzieląc strunę w różnych stosunkach. Stwierdził, że najlepsze, tzn. „najmilsze dla ucha” harmonie wyrażone są poprzez najprostsze proporcje, którym odpowiadają ułamki mające w mianowniku kolejne liczby naturalne, a w liczniku jeden. Odkrył w ten sposób tzw. szereg alikwotów, który stanowi fundament naszego systemu muzycznego.
Działania w zbiorze liczb niewymiernych
Oczywiście w starogreckim systemie tonalnym, który dopuszczał współbrzmienia mniejsze niż półtony odkrycie Pitagorasa świetnie się sprawdzało. Niestety, gdy próbujemy jego odkrycie przenieść do dobrze nam znanego (bardziej lub mniej świadomie) systemu równomiernie temperowanego, tzn. takiego, którym muzycy posługują się mniej więcej od XVII wieku, pojawiają się pewne problemy.
System równomiernie temperowany polega na podziale oktawy na 12 równych półtonów, co najlepiej obrazuje klawiatura fortepianu, gdzie między kolejnymi klawiszami jest taka sama odległość, a co dwunasty daje nam współbrzmienie oktawy. Ma też tę niezwykłą własność, że poruszając się po klawiaturze kwintami (7 półtonami), np. od dźwięku C, po 12 kwintach trafimy ponownie na C (ale siedem oktaw wyżej). Taki ciąg muzycy określają mianem koła kwintowego. Jeśli jednak zastosujemy się do obliczeń Pitagorasa, który kwintę określił jako stosunek 3/2 i podniesiemy tę wartość do potęgi 12 (tyle kwint potrzebujemy), to otrzymamy liczbę ok. 129,746. A przecież spodziewaliśmy się otrzymać siódmą potęgę dwójki, czyli interwału oktawy, dokładnie = 128. Jeśli podzielimy przez siebie otrzymane wyniki, to uzyskamy wielkość ok. 1,014, co równa się w przybliżeniu ćwierci tonu i jest znane jako komat pitagorejski – na cześć „drobnej” nieścisłości w obliczeniach genialnego matematyka.
Obecnie mamy jednak nad Pitagorasem tę przewagę, że potrafimy posługiwać się liczbami niewymiernymi, czyli takimi, których nie można przedstawić w postaci ułamka dwóch liczb całkowitych (co przeczy właściwie harmonii sfer). To dzięki tej wiedzy możemy znaleźć odległość półtonu, dzieląc oktawę na 12 równych części poprzez równanie:
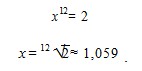
Pierwiastek z 2 jest liczbą niewymierną, co można udowodnić wykorzystując, jak na ironię, twierdzenie Pitagorasa. Wykorzystanie liczb niewymiernych jednak, to jedyny sposób, aby stosunkowo najlepiej rozwiązać ten zawiły matematyczno-muzyczny problem.
Działania na ułamkach
Z pomocą matematyki można usystematyzować przecież nie tylko zależności harmoniczne, ale również tak istotny element muzyki jak rytm. Systemem podziału wartości rytmicznych oraz opisem metrum zajęto się szczegółowo w średniowieczu pod koniec XIII wieku. Sposób notacji rytmu, zwany notacją menzuralną opisał Philippe de Vitry w traktacie Ars nova. Idea ta sprowadza się tak naprawdę do dzielenia kolejnych wartości rytmicznych na trzy (perfectum) lub dwie (imperfectum) mniejsze. Średniowieczne podziały metryczne były notowane przy kluczu za pomocą systemu składającego się okręgu, półokręgu i kropki. Obecnie posługujemy się notacją metrum, która bardziej przypomina matematyczne ułamki. Zasada zapisu metrum jest bardzo łatwa jeśli rozumie się prawa dodawania ułamków. Całej nucie przyporządkowana jest liczba 1, półnucie, czyli połowie całej nuty liczba 1/2, a ćwierćnucie, która jest ćwiartką całej nuty 1/4, czyli każda kolejna wartość jest połową poprzedniej. Jeśli kompozytor chce napisać w takcie trzy półnuty, to mnoży 1/2 ∙ 3, uzyskując 3/2, co przy kluczu na pięciolinii zapisuje się bez kreski ułamkowej. Jeśli muzyk jest dobry w dodawaniu ułamków, to powinien wiedzieć, że w takim takcie może zapisać np. 2 ćwierćnuty, 4 ósemki i 8 szesnastek, ponieważ 2 ∙ 1/4 + 4 ∙ 1/8 + 8 ∙ 1/16 = 24/16 = 3/2. Dobry kompozytor musi zatem sprawnie operować ułamkami. Należy jednak pamiętać, że w takcie ważne jest również akcentowanie, które powoduje, że dla muzyka 3/4 to zupełnie co innego niż 6/8, choć według matematycznych prawideł wartości te są sobie równe.
Geometria kompozycji
Choć kompozytorzy może nie zawsze są świadomi związków muzyki z matematyką, to jednak chętnie korzystają w swoich utworach z przekształceń geometrycznych. Takie zabiegi w nomenklaturze muzycznej są nazywane technikami kontrapunktycznymi. Należy do nich m.in. rak, czyli symetria względem osi pionowej do pięciolinii, która oznacza, że pewien fragment melodii, zostaje w dalszej części kompozycji zapisany od końca – w odbiciu lustrzanym. Można również zastosować w utworze symetrię względem osi poziomej. Wtedy mówimy o inwersji, czyli odwróceniu kierunku prowadzenia linii melodycznej. Do technik kontrapunktycznych należą także augmentacja i dyminucja, które są równoważne mnożeniu wartości rytmicznych przez skalar, tzn. odpowiednio ich wydłużaniu i skracaniu. Transpozycję można natomiast utożsamiać z przesunięciem melodii o wektor dodatni, którego długość wyznacza pewien interwał.
Muzyczne łamigłówki
Jest coś jeszcze, co łączy muzyków i matematyków – to zamiłowanie do łamigłówek. Z tą jednak różnicą, że gdy matematycy uwielbiają rozwiązywać skomplikowane zadania, muzycy wolą je układać. Czyniło tak wielu kompozytorów, szczególnie w epoce renesansu, gdzie zagadki muzyczne były popularną formą rozrywki. Zabawy te nazywano sztuczkami niderlandzkimi, gdyż zazwyczaj pojawiały się one w twórczości kompozytorów z tamtego regionu. Często polegały na tym, że np. klucz zapisywano w postaci znaku zapytania, co powodowało, że utwór można było odczytać na kilka sposobów. Popularne było także zjawisko gematrii wykorzystujące w kompozycjach liczby, które odpowiadały kolejnym literom alfabetu, np. Johannes Ockeghem, często opierał budowę cantus firmus na liczbie 23, która odpowiadała sumie jego inicjałów (J – 9, O – 14). Ciekawą rozrywkę wymyślili też kompozytorzy osiemnastowieczni i to tak poważni jak Haydn czy Mozart. Określali swoje łamigłówki mianem Musikalisches Würfelspiel. Twórcy pisali po 11 wersji kolejnych taktów kompozycji. Gra polegała na tym, żeby rzucając kośćmi, losować kolejne takty kompozycji i w ten sposób tworzyć nową. Oczywiście ciekawscy matematycy zauważą natychmiast, że takty o numerach 7 będą wypadać częściej niż np. o numerze 12 (o czym mówi nam rachunek prawdopodobieństwa).
Skoro już o zagadkach i szyfrach mowa, to warto również wspomnieć o zjawisku szczególnie powszechnym w epoce baroku, mianowicie o basie cyfrowanym. Był to bardzo pomysłowy sposób zapisu akompaniamentu, wykonywanego m. in. na klawesynie, organach czy lutni. W systemie tym umieszczano tylko pojedyncze dźwięki najniższego głosu, natomiast pod nimi podpisywano cały szereg cyfr, które wprawny wykonawca z łatwością rozszyfrowywał i przekładał na akordy.
Kombinatoryka, czyli ile to jest „12!”
Prawdziwe pole do popisu przyniósł kompozytorom-matematykom wiek XX. Najwięcej, bo aż 479 001 600 możliwości różnych kombinacji przyniosła twórcom technika dodekafoniczna. Skąd taka gigantyczna liczba? Wszystko zaczęło się od pomysłu Arnolda Schönberga, który postanowił zastosować serię 12 dźwięków tak, aby żaden dźwięk w serii się nie powtarzał. Wchodzimy tu na grunt kombinatoryki, a dokładnie obliczania permutacji. Permutacja to po prostu przestawienie elementów w pewnym ciągu. Dla Schönberga ciąg to właśnie seria, a jego elementami są dźwięki. Liczbę permutacji ciągu, w tym przypadku złożonego z 12 elementów, możemy łatwo obliczyć: na pierwszym miejscu serii mamy do wyboru 12 dźwięków, na drugim już tylko 11, bo nie wolno powtórzyć dźwięku poprzedniego, następnie 10, 9 i.t.d. aż do 1. Wszystkie te liczby należy pomnożyć i ostatecznie otrzymamy wartość, którą matematycy opisują jako 12! (12 silnia), która odpowiada liczbie 479 001 600.
Jeszcze więcej kombinacji stworzył serializm, będący konsekwencją dodekafonii. Polegał na przyporządkowaniu dwunastu wysokościom dźwięku szeregu różnych własności, takich jak dynamika, wartości rytmiczne, artykulacja. Możliwości różnych układów stały się wtedy praktycznie nieograniczone.
Matematyczne inspiracje
Dla wielu kompozytorów XX wieku matematyka była po prostu źródłem inspiracji. Najpełniej zaawansowane narzędzia matematyczne wykorzystał w swojej twórczości Iannis Xenakis, kompozytor greckiego pochodzenia. Był on jednocześnie architektem, więc jego wiedza w dziedzinie matematyki wykraczała znacznie poza zakres szkolnego nauczania. Xenakis w swych utworach bazował na tak złożonych zagadnieniach, jak procesy stochastyczne, teoria zbiorów czy teoria gier, które są trudne do zrozumienia nawet studentom matematyki.
Wśród dwudziestowiecznych kompozytorów znajdą się także inni prawdziwi pasjonaci matematyki. Pierre Boulez w szkole wykazywał szczególne zdolności w tym kierunku i zapisał się nawet na wyższy kurs matematyki, jednak w 1942 rozpoczął studia w Paryskim Konserwatorium i całkowicie poświęcił się muzyce. Również Witold Lutosławski studiował matematykę na Uniwersytecie Warszawskim równolegle z kompozycją w konserwatorium. Studia matematyczne przerwał jednak po roku, również skupiając się wyłącznie na muzyce. Czyżby zatem to jednak muzyka miała większą siłę przyciągania?
Algorytm kompozycji?
XX wiek to także muzyka elektroniczna i komputerowa, w której zaczęto dosłownie stosować język matematyki, czyli algorytmy. Jednak pojawiło się pytanie, na ile maszyna może zastąpić prawdziwego, żywego kompozytora? Wielu pomysłowych konstruktorów próbowało tworzyć mechanizmy, które umożliwiłyby komponowanie bez udziału człowieka i to na długo przed wynalezieniem komputera. Dietrich Nikolaus Winkel skonstruował w 1821 roku instrument, nazwany componium. Były to automatyczne organki, które losowo odtwarzały warianty pewnej kompozycji. W późniejszych komputerach zaczęto stosować bardziej złożone programy, które wykorzystywały łańcuchy Markowa, używane w statystyce, aby na podstawie poprzednich dźwięków badać, jaki powinien być następny. Wszystkie te zabiegi są jednak tylko przedłużeniem procesu twórczego, a nie prowadzą do samoistnego powstania dzieła.
Patrząc z perspektywy historycznej można zauważyć, że muzyka nie może się obejść bez matematyki. Czy można zatem pokusić się o napisanie algorytmu kompozycji? Jaki wzór podać na powstanie arcydzieła? Od jakich zmiennych zależy sukces kompozytora? Niestety wkraczamy tu na bardzo niepewny dla matematyka grunt pojęć niedefiniowalnych, takich jak inspiracja, emocje czy wrażliwość. To właśnie one nadają ostateczny kształt muzyce. Czyżby matematyka miała zatem ulec wobec nieskończonej wyobraźni kompozytora? Ależ skąd! Przecież nieskończoność jest pojęciem matematycznym.
















